Matematika 2020.04.29. (118.óra) - András bá

2020.04.29.                        118.óra

Ismerkedés a gúlával

(Tk.:111 - 113.o.) 

1.) Ismétlés

     - a test felszíne: a testet határoló oldallapok területeinek 

       összege (jele: A)
     - a test térfogata: a körülhatárolt térrész nagyságát
       jellemzi (jele: V)
     - szabályos testek: olyan, sokszöglapokkal határolt 
       konvex test, amelynek élei, élszögei és lapszögei 
       egyenlők. Mindegyik szabályos testet egybevágó 
       szabályos sokszögek határolják.  
       (szabályos tetraéder, szabályos hexaéder (kocka), 
        szabályos oktaéder, szabályos dodekaéder, 
        szabályos ikozaéder)
     - A hasáb felszíne a határoló lapok területének, azaz az
       alaplapok területének (T_a) és a palást területének (T_p) 
       az összege: A = 2T_a + T_p
      - A hasáb térfogata: alaplap területe ⋅ testmagasság:
                                               V = T_{a ⋅ M}

                
    -------------------------------------------------------------------------
      - téglatest: Olyan egyenes hasáb, amelynek alaplapja 
                        téglalap. (Minden lapja téglalap.)

              - felszíne:  A = 2(ab + ac + bc)

              - térfogata: V = abc

                    
                   
     -------------------------------------------------------------------------
      - kocka: Olyan egyenes hasáb, amelynek minden éle
                   egyenlő és oldallapjai négyzetek.
            - felszíne: A = 6a²
            - térfogata: V = a³
                
     -------------------------------------------------------------------------
      - négyzet alapú egyenes hasáb (négyzetes oszlop):
        Olyan téglatest, amelynek alaplapja négyzet.
            - felszíne:  A = 2a²+ 4aM = 2a(a + 2M)
            - térfogata:  V = a²M
              
     -------------------------------------------------------------------------
      - henger: (idegen szóval cilinder) térbeli test. A henger
                      alapját egy görbe, a vezérgörbe adja. 
                     Többnyire olyan hengerről van szó, aminek
                     alapját ellipszis, speciális esetben kör alkotja.
                     Legtöbbször ezt nevezik hengernek.
               felszíne: A = 2r² 𝛑+ 2rM = 2r𝛑 (r+ M)
                      térfogata: V = r² 𝛑 M
                           
     --------------------------------------------------------------------------
 2.) Gúla 

 Ötszög alapú szabályos gúla

 

 

A gúlát egy sokszög, és annyi háromszög határolja, ahány oldalú a sokszög.

A sokszög a gúla alaplapja, a háromszögek a gúla oldallapjai.

Az alaplapot határoló élek az alapélek.

Az oldallapok az oldalélekben találkoznak.

Az oldalélek egy pontban, a gúla csúcspontjában futnak össze.

Az oldallapok együtt a gúla palástját alkotják.

A gúla magassága a gúla csúcsa és az alaplap síkjának a távolsága, vagyis a csúcsból az alaplap síkjára állított merőleges szakasz hossza.

Ha a gúla alaplapja szabályos sokszög, és a magasságának talppontja az alaplap középpontjában van, akkor szabályos gúlának nevezzük.

A háromoldalú gúla neve: tetraéder. A szabályos tetraéder olyan gúla, amelynek minden lapja szabályos háromszög. 

                 

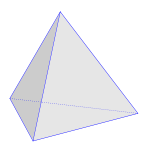
A gúla felszíne az alaplap területének (T_a) és az oldallapok területének, vagyis a palást területének (T_p) az összege:

A = T_a + T_p

A gúla térfogata az alaplapjával és a testmagasságával megegyező alaplapú és magasságú hasáb térfogatának a harmada:                                                  _{V = T𝚊 ⋅ M : 3𛲡}

                
 3.) Video  A GÚLA FOGALMA, ELEMEI ÉS FAJTÁI (1. RÉSZ)(8:40)


4.) Video   A GÚLA FOGALMA, ELEMEI ÉS FAJTÁI (2. RÉSZ)(7:51)